SOLUTION:
Case: Probability
Given:
Incidence rate = 0.8%
False negative = 6%. hence True negative is = (100% - 6%) which is 94%
False positive = 3%, hence true positive is = (100% - 3%) = 97%
FN = False negative
TN= True negative
FP= False positive
TP= True positive
Required: To find the probability that a person who tests positive actually has the disease.
Method:
The chances that someone who test positive actually has the diseases will be given as:
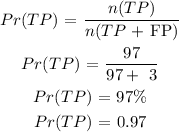
Final answer:
The probability that a person who tests positive actually has the disease is 0.970