Question

The height of a triangle is 2 feet more than four times the base. The area of the triangle is 10 feet squared. Find the dimensions of the triangle

Answer 1

Let b be the base and h be the height

h = 2 + 4b

area = 10

`\text{Area of a triangle = }(1)/(2)* b* h`
`10=(1)/(2)* b*(2+4b)`
`10=(b(2+4b))/(2)`

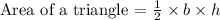
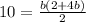
Multiply bothside by 2

`20=b(2+4b)`
`20=2b+4b^2`
`4b^2+2b\text{ - 20 =0}`

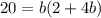
Using factorization method to solve the above

Find two numbers such that its sum give 2 and its product gives -80

The two numbers are 10 and -8

Replace 2 by 10 and -8 in the expresion

`4b^2+\text{ 10b-8b -20 = 0}`

`2b(2b+\text{ 5) - 4(2b+}5)=0`
`(2b+5)(2b-4)=0`

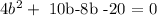
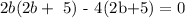
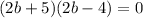
2b + 5 = 0 or 2b - 4 =0

2b = -5

b = -5/2 or 2b = 4

b = 2

since there is no negative length, then base is 2 feet

To get the height, substitute h = 2 + 4b

h = 2+ 4(2)

= 2 + 8

= 10

Height is 10 feet

The dimensions of the triangle is;

height = 10 feet

base = 2 feet