Question

Given f(x) = (lnx)^3 find the line tangent to f at x = 3

Answer 1

Step-by-step explanation

We must the tangent line at x = 3 of the function:

`f(x)=(\ln x)^3.`

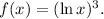
The tangent line is given by:

`y=m*(x-h)+k.`

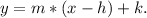
Where:

• m is the slope of the tangent line of f(x) at x = h,

,

• k = f(h) is the value of the function at x = h.

In this case, we have h = 3.

1) First, we compute the derivative of f(x):

`f^(\prime)(x)=(d)/(dx)((\ln x)^3)=3*(\ln x)^2*(d)/(dx)(\ln x)=3*(\ln x)^2*(1)/(x)=(3(\ln x)^2)/(x).`

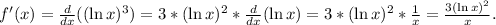
2) By evaluating the result of f'(x) at x = h = 3, we get:

`m=f^(\prime)(3)=(3)/(3)*(\ln3)^2=(\ln3)^2.`

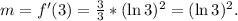
3) The value of k is:

`k=f(3)=(\ln3)^3`

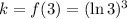
4) Replacing the values of m, h and k in the general equation of the tangent line, we get:

`y=(\ln3)^2*(x-3)+(\ln3)^3.`

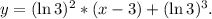
Plotting the function f(x) and the tangent line we verify that our result is correct:

Answer

The equation of the tangent line to f(x) and x = 3 is:

`y=(\ln3)^2*(x-3)+(\ln3)^3`