Question

Use the sequence below to complete each task. 972, 324, 108, ... a Identify the common ratio (r). b. Write an equation to represent the sequence. C. Find the 6th term (as)

Answer 1

The ratio of a sequence can be found by dividing a term by its previous, we have:

`r\text{ = }(324)/(972)=(1)/(3)`

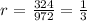
If this is a geometric sequence the ratio should be the same for all the terms, so let's test with the other pair of terms:

`r=(108)/(324)=(1)/(3)`

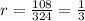
Since the ratio is the same it is a geometric sequence. We can then write the expression to represent it as shown below:

`a_n=972\cdot(1)/(3)^(n-1)`

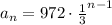
To find the 6th term we need to use n as equal to 6 in the expression above, we have:

`\begin{gathered} a_6=972\cdot(1)/(3)^(6-1) \\ a_6=972\cdot(1)/(729)=1(1)/(3) \end{gathered}`

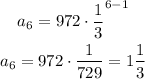
The sixth term is 1 1/3 or 1.33333...