Part (a) We are given that an object at a constant speed moves down an inclined surface. We are asked to determine the work done by the friction force. To do that we will first determine the magnitude of the friction force using the following formula:
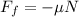
Where:

Now we need to determine the magnitude of the normal force. To do that we will first do a free body diagram, like this:
From the diagram, we do a sum of forces in the perpendicular direction of the inclined plane. For convenience, we will call this direction the y-direction. We get:
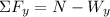
Since there is no movement in the y-direction the sum of forces must be equal to zero, therefore:
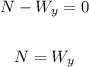
Therefore, the normal force is equivalent to the y-component of the weight. To determine this component we use the following triangle:
Therefore, we can use the trigonometric function cosine since it is defined as:
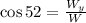
Now we multiply both sides by "W":
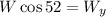
Now we replace this in the formula for the normal force:
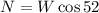
Now we replace this in the formula for the friction force:
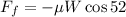
Since the weight is the product of the mass by the acceleration of gravity we get:
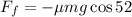
Now, the work is the product of the force by the distance:
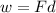
Therefore, to determine the work done by friction we need to multiply the formula for the friction by the distance "d":
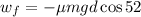
Now we have a formula for the work done by friction. Now we plug in the values:
![w_f=-(0.1)(90\operatorname{kg})(9.8(m)/(s^2))(30m)\cos 52]()
Now we solve the operations and we get:
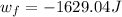
Part (b) Now we are asked to determine the work done by the rope, this is equivalent to the work done by the tension force. Therefore, we need to determine the magnitude of the tension. To do this we will add the forces in the direction parallel to the inclined plane. For convenience, we will call this direction the x-direction. Therefore, we have:
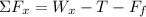
Since the velocity is constant this means that the acceleration is zero, and therefore, the total forces add up to zero, therefore, we have:
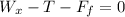
Now we solve for the tension force "T", we get:
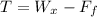
Now we use the previous triangle we use to obtain the y-component of the weight to determine the x-component of the weight. In this case, we use the trigonometric function sine:
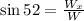
Now we multiply both sides by "W":
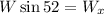
Now we replace in the formula for the tension:
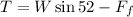
Now we replace the weight for the product of the mass by the acceleration of gravity:
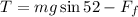
Now we multiply by the distance to obtain the work:
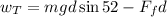
Now we plug in the values:
![w_T=(90\operatorname{kg})(9.8(m)/(s^2))(30m)\sin 52-1629.04J]()
Now we solve the operations:
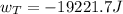
We use a negative sign since the tension acts against the movement.
Part (c) Now we are asked to determine the work done by gravity. This is equivalent to the work done by the x-component of the weight. The x-component is given by:
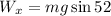
Now we multiply by the distance:
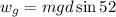
Now we plug in the values:
![w_g=(90\operatorname{kg})(9.8(m)/(s^2))(30m)\sin 52]()
Solving the operations we get:
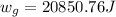
Part (d) Now we are asked to determine the total work. This is determined by adding the work done by all the forces, we get:
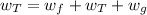
Now we plug in the values:
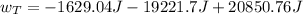
Solving the operations we get:
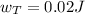
Therefore, the total work is 0.02 Joules. But this is due to the approximations we did when finding the results. Since the object moves at a constant velocity, then the total work is zero.