ANSWER
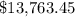
Step-by-step explanation
We want to find the amount she will have after 5 years.
To do this, we apply the compound interest formula:

From the question:
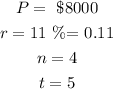
n is 4 because there are 4 quarters in a year.
Therefore, we have that in 5 years, the amount she will have is:
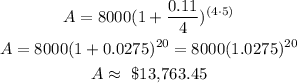
That is how much she will have in 5 years.