The probability of A or B when you have mutually exclusive events (ones that can't happen at the same time) is:
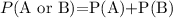
Let's call A the probability of getting a 4, B the probability of getting a 5 and C the probability of getting a 6.
Then in the deck, there are 4 cards with the number 4, then the probability of A is:
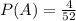
There are 4 cards with the number 5, and 4 cards with the number 6, then the probabilities of B and C are:
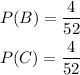
Thus, the probability of A or B or C is:
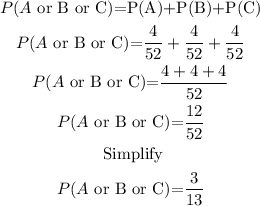
Answer: The probability of that card being a 4, 5 or 6 is 3/13