Given:
There are given that the first pool contains 1150 liters of water and the second pool contains 1300 liters of water.
Step-by-step explanation:
Let P1 represent the first pool and P2 represent the second pool and t is represent the time in minutes.
Then,
From the first pool:

And,
From the second pool:
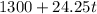
Now,
Equal both of the equations:
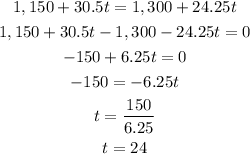
And,
The volume of the water in both of pool is:

Final answer:
Hence, there are 24 minutes will the pools have the same amount of water and the volume of the water will be 1882 liters.