As given by the question
There are given that the golf ball covers a horizontal distance of 301.5 m.
Now,
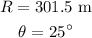
The vertical motion is:
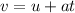
Where
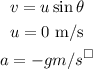
Put the value
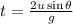
Then,
The range of projectile motion :
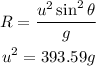
And,
The height
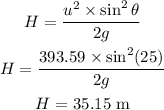
Hence, the maximum height that can reach by the ball is 35.15 m