Answer:
It takes the younger gardener about 49.11 minutes while it takes the older gardener about 77.11 minutes.
Explanation:
Let the time taken by the younger gardener = x minutes
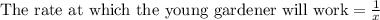
The older gardener takes 28 minutes more than the younger gardener, therefore:
The time taken by the older gardener = (x+28) minutes
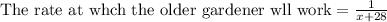
If they work together, it takes 30 minutes.
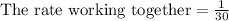
Therefore:
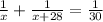
We solve the equation for x:
![\begin{gathered} ((x+28)+x)/(x(x+28))=(1)/(30) \\ (2x+28)/(x(x+28))=(1)/(30) \\ \text{ Cross multiply} \\ 30(2x+28)=x(x+28) \\ \text{ Open the brackets} \\ 60x+840=x^2+28x \\ x^2+28x-60x-840=0 \\ x^2-32x-840=x \end{gathered}]()
We then solve the quadratic equation for x using the quadratic formula:
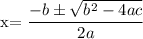
In our equation:a=1, b=-32, and c=-840
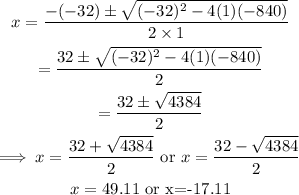
Since time cannot be negative: x=49.11 minutes.
Thus, the time it takes:
• The younger gardener = 49.11 minutes
,
• The older gardener = 77.11 minutes
It takes the younger gardener about 49.11 minutes while it takes the older gardener about 77.11 minutes (correct to 2 decimal places).