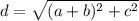Question

Find the lengths of the diagonals of this trapezoid. (image attached)thank you ! :)

Answer 1

Given:

There are given that the trapezoid with vertices:

Step-by-step explanation:

To find the length of the diagonals, we need to use the distance formula:

So,

From the distance formula:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

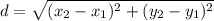
Now,

The length of diagonal from point (-b, c) to (a, 0):

So,

Using the distance formula:

Then,

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ d=√((a+b)^2+(0-c)^2) \\ d=√((a+b)^2+c^2) \end{gathered}`

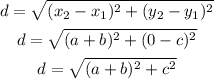
And,

The length of diagonal from point (b, c) to (-a, 0) is given by:

`\begin{gathered} d=√((-a-b)^2+(0-c)^2) \\ d=√((a+b)^2+c^2) \end{gathered}`

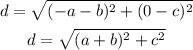
Final answer:

Hence, the distance of the given trapezoid is the same for both the diagonal.

`d=√((a+b)^2+c^2)`