Question

Geometry***please help me find the surface area of this figure

Answer 1

We will determine the surface area of the cylinder as follows:

*First: We find the area of one of the bases [For each cylinder]:

**Bigger cylinder:

`A_(bC)=\pi(4)^2\Rightarrow A_(bC)=16\pi`

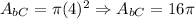
**Smaller cylinder:

`A_(bc)=\pi(1)^2\Rightarrow A_(bc)=\pi`

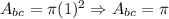
*Second: We determine the area of the face of the cylinder. For this, we can see the following:

When we "unroll" the face of the cylinder we will obtain a rectangle, and thus we find its area, that will be given by the circumference of the base of the cylinder times the length of the cylinder.

**Circumference bigger cylinder:

`C_(bc)=2\pi(4)\Rightarrow C_(bc)=8\pi`

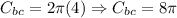
**Circumference smaller cylinder:

`C_(sc)=2\pi(1)\Rightarrow C_(sc)=2\pi`

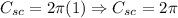
*Third: We find the area for each face of each cylinder:

**Area rectangle bigger cylinder:

`A_(rC)=8\pi\cdot6\Rightarrow A_(rC)=48\pi`

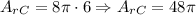
**Area rectangle smaller cylinder:

`A_(rc)=2\pi\cdot1\Rightarrow A_(rc)=2\pi`

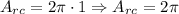
*Fourt: We will determine the total surface area for the shape by adding the areas for the bigger cylinder and substract from it the surface area for the smaller cylinder, that is:

`T_s=(16\pi+48\pi)-(\pi+2\pi)\Rightarrow T_s=61\pi`

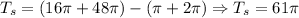
So, the total surface area for the hollow cylinder is 61pi square inches.