Question

Find the equation of the line with slope = -4 and passing through the point (8,-10). Point-Slope Form: y - y1 = m(x - x1) Slope-Intercept Form: y = mx + b

Answer 1

To determine the equation of a line given that you know its slope and a point you can use the point-slope form:

`y-y_1=m(x-x_1)`

Where

m represents the slope of the line

(x₁,y₁) represents the coordinates of the point crossed by the line

We know that the slope of the line is m=-4 and the coordinates of the point are x₁=8 and y₁=-10, replace these values in the point-slope form:

`\begin{gathered} y-(-10)=-4(x-8) \\ y+10=-4(x-8) \end{gathered}`

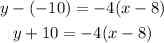
To write the equation in slope-intercept form, first, distribute the multiplication on the parentheses term:

`\begin{gathered} y+10=-4\cdot x+(-4)(-8) \\ y+10=-4x+32 \end{gathered}`

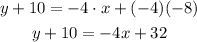
Next, pass 10 to the right side of the equation by applying the opposite operation "-10" to both sides of it:

`\begin{gathered} y+10-10=-4x+32-10 \\ y=-4x+22 \end{gathered}`

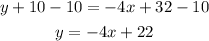
The equation of the line is y=-4x+22