The roots of the quadratic function are given as,

Sum of roots is calculated as,
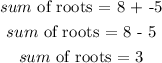
The product of roots is calculated as,
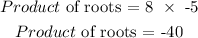
The required quadratic function is given as,
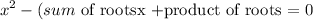
A required quadratic function is calculated as,
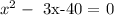
Thus the required quadratic function is,
