we are given the following functions:
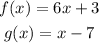
We are asked to determine:
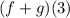
To do that, let's remember the following relationship:
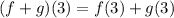
Therefore, we need to substitute x = 3 in each function. Substituting in f(x):
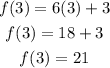
Substituting in g(x):
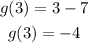
Adding both functions:
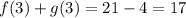
Therefore, the answer is 17.