Question

determine whether AB and MN are parallel, perpendicular, or neither, A(-4,-8) B(4,-6) M(-3,5) N(-1,-3) A.neither B.parallel C.perpendicular

Answer 1

for this, we will find the slope of both the lines AB and MN

the slope of AB is

`\begin{gathered} m=(-6-(-8))/(4-(-4)) \\ m=(2)/(8)=(1)/(4) \end{gathered}`

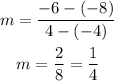
the slope of MN is,

`\begin{gathered} m=(-3-5)/(-1-(-3)) \\ m=(-8)/(2)=-4 \end{gathered}`

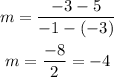
both the slopes are different, so line AB and MN is not parallel.

but

`-4*(1)/(4)=-1`

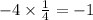
the multiplication of both the slope is -1 so line AB and MN is perpendicular to each other.

option C is correct.