Question

200 lottery tickets are sold for $2 each. The person with the single winning ticket will get $83. What is the expected value for a ticket in this lottery?

Answer 1

Given:

200 lottery tickets are sold for $2 each

winning ticket will get $83

To determine the expected value, we must the chance of winning the prize first:

The change of winning the price is 1/200.

So, the first expression would be:

`(83-2)((1)/(200))`

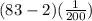
Next, we determine the lose as well.

The chance to lose is (199/200). So the second expression is:

`-2((199)/(200))`

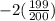
Then, we combine the two expressions:

`\begin{gathered} (83-2)((1)/(200))-((2)(((199)/(200)) \\ \text{Simplify} \\ =(81)/(200)-(199)/(100) \\ =-1.585 \end{gathered}`

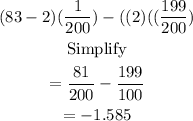
Therefore, the expected value for a ticket is -$1.585 or the person is expected to lose $1.585.