Question

Triangle FGH has vertices F(−2, 0), G(0, 2), and H(2, 0). A dilation, centered at the origin, is applied to this triangle. The image has vertices F′(−14, 0), G′(0, 14), and H′(14, 0).What is the scale factor of this dilation?Enter your answer in the box.

Answer 1

7

Step-by-step explanation:

Step 1. The first step is to make a diagram of the points and connect them to form the triangles.

In the following diagram, we have the original points FGH in BLUE and the image points F'G'H' in RED:

Step 2. Compare the length of two corresponding sides.

Let's take the base of each triangle.

The base of the red triangle and the base of the blue triangle is shown in the image:

Step 3. To find the scale factor, divide the new length over the original length:

`\text{scale factor=}(28)/(4)`

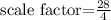
The result is:

`\text{scale factor=}7`

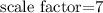
Answer:

7