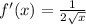Given:
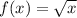
Required:
To find the derivative of the given function by using the first principle.
Step-by-step explanation:
To find the derivative by the first principle we will use the limit method.
![\begin{gathered} f^(\prime)(x)=\lim_(h\to0)(f(x+h)-f(x))/(h) \\ f^(\prime)(x)=\operatorname{\lim}_(h\to0)(√(x+h)-√(x))/(h) \end{gathered}]()
Rationalise the denominator
![f^(\prime)(x)=\operatorname{\lim}_(h\to0)(√(x+h)-√(x))/(h)*(√(x+h)+√(x))/(√(x+h)+√(x))]()
Use the formula:
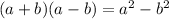
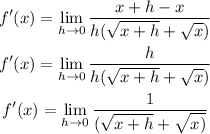
Now apply the given limit
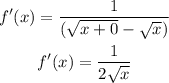
Final answer:
Thus the derivative of the given function is