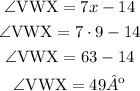Question

Jan 28,94037 AMUutch helps VideoMAUVW, U is extended through point W to point X,mVWT = (Pilt 14), m_WUV = (2x + 11) andm UVW = (36 – 7° Mnd m_VWTSubmit Answerattempt touto

Answer 1

Given ΔUVW, segment UW is extended to point X

And the following angles are known

∠VWX=(7x-14)º

∠WUV=(2x+11)º

∠UVW=(3x-7)º

You have to find ∠VWX

First, let's make a sketch of the triangle and place the angles

To determine ∠VWX, first, we need to find the value of x.

For this, we have to apply the exterior angle theorem, which states that the measure of one exterior angle of a triangle is equal to the sum of the opposite interior angles, so that:

`\begin{gathered} \angle\text{VWX}=\angle\text{WUV}+\angle\text{UVW} \\ (7x-14)º=(2x+11)º+(3x-7)º \end{gathered}`

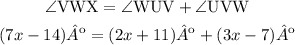
From this expression, we can determine the value of x.

1) Erase the parentheses and on the right side of the equation order the like terms and simplify them:

`\begin{gathered} 7x-14=2x+11+3x-7 \\ 7x-14=2x+3x+11-7 \\ 7x-14=5x+4 \end{gathered}`

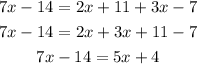
2) Now you have to pass 5x to the left side of the expression and -14 to the right side. For this, apply the opposite operation to both sides of it.

For "5x" you have to subtract it and for "-14" you have to add it as follows:

`\begin{gathered} 7x-5x-14=5x-5x+4 \\ 2x-14=4 \\ 2x-14+14=4+14 \\ 2x=18 \end{gathered}`

3) Divide both sides by 2 to determine the value of x

`\begin{gathered} (2x)/(2)=(18)/(2) \\ x=9 \end{gathered}`

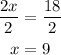
Now we can calculate the measure of ∠VWX

`\begin{gathered} \angle\text{VWX}=7x-14 \\ \angle\text{VWX}=7\cdot9-14 \\ \angle\text{VWX}=63-14 \\ \angle\text{VWX}=49º \end{gathered}`