Question

In a raffle where 7000 tickets are sold for $2 each, one prize of $9000 will be awarded. What is the expected value of a single ticket in the raffle?

Answer 1

The expected value of a single ticket in the raffle = -1.36

Step-by-step explanation

The expected of a single ticket in the raffle can be calculated using:

`\begin{gathered} E(x)=\sum ^{}_{}x\mathrm{}p(x) \\ \text{Where x is the random variable and } \\ \text{P(x) is the probability of the random variable x} \end{gathered}`

Since 7000 tickets are sold for $2 each, total amount of tickets sold would be = 7000 x 2 = $14,000

The probability of winning =

`(1)/(14000)`

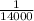
The probability of losing =

`1-(1)/(14000)=(13999)/(14000)`

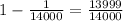
The gain or loss of winning =

`9000-2=8998`

The gain or loss of losing = -2

Therefore, the expected value E(x) of a single ticket in the raffle =

`\begin{gathered} E(x)=8998((1)/(14000))+(-2)(13999)/(14000) \\ E(x)=(8998)/(140000)-(27998)/(14000) \\ E(x)=-(19000)/(14000) \\ E(x)=-1.36 \end{gathered}`