Question

the cable of a suspension bridge forms a parabola, of which the lowest part of the cable is 3 m above the surface of the bridge. The bridge is 90 M long and has a 8 m high Towers at the end of the bridge that supports the suspension cable at the top of each tower. if a quadratic function can model the cable, what would be coffient of x^2

Answer 1

The coefficient of x^2 is;

`a=(1)/(405)`

Step-by-step explanation:

Given that the lowest point of the cable is 3m above the surface of the bridge.

The bridge is 90 m long and has a 8m high towerat each edge.

Let us represent the question on a drawing;

From the drawing above, we assumed that the coordinates of the lowest point is (0,0);

`(h,k)=(0,0)`

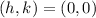
Recall that the formula for vertex equation is;

`y=a(x-h)^2+k`

substituting the value of h and k;

`\begin{gathered} y=a(x-0)^2+0 \\ y=ax^2\text{ -------1} \end{gathered}`

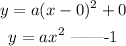
From the derived equation 1, we can find the value of a which is the coefficient of x^2 by substituting the corresponding values of x and y at a particular point on the graph.

At the end of the bridge, the coordinate of the top right edge is;

`(x,y)=(45,5)`

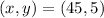
substituting into the equation;

`\begin{gathered} y=ax^2 \\ a=(y)/(x^2) \\ a=(5)/(45^2) \\ a=(1)/(405) \end{gathered}`

Therefore, the coefficient of x^2 is;

`a=(1)/(405)`