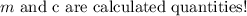Question

I. Find the slope of the line containing each pair of points.1. (5,0) and (6,8)2. (4, -3) and (6,-4)3. (-2, 4) and (-9, -T)II. Find the slope of each line.4. y = 75. x= -46. 2x + y = 157. x - 2y = 7III. Find the equation of the line with the given slope through the given point in slope-intercept form.4.8. m = 4; (3,2)9. m = -2; (4,7)10. ma-:13,3IV. Find the equation of the line containing the following points in standard form.11. (2,6) and (4,1)12. (3,5) and (-5,3)

Answer 1

We will investigate the how to formulate an equation of a straight line.

All equation of straight line have a general slope-intercept format given as follows:

`y\text{ = m}\cdot x\text{ + c}`

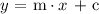
Where,

`\begin{gathered} m\colon\text{ Slope} \\ c\colon\text{ y-Intercept} \end{gathered}`

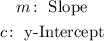
To completely define any equation of a line we need to two points OR we need a point and one of the parameters ( m or c )!

We will suppose that we have two points ( A and B ) as follows:

`\begin{gathered} A\colon(x_1,y_1) \\ B\colon(x_2,y_2) \end{gathered}`

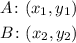
To determine the value of parameter slope ( m ) we utilize the following general formula:

`m\text{ = }(y_2-y_1)/(x_2-x_1)`

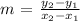
We simply plug in the respective values of the coordinates ( A and B ) in the general formula above and solve for ( m ).

Once we have evaluated the value of parameter ( m ) in the previous step we will determine the value of parameter ( c ) i.e y-intercept.

To determine the value of ( c ) we need only one point! You can choose either point ( A or B )!

Lets assume that we chose point ( A ). We will then plug in the values of coordinates and the value of parameter ( m ) into the general form of the equation as follows:

`y_1\text{ = m}\cdot x_1+c`

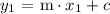
In the above form all are known quantities and only ( c ) is unknown! We can manipulate the above expression and solve for ( c ) as follows:

`c\text{ = }y_1\text{ -m}\cdot x_1`

Then we have obtained the value of ( c ) as well!

We can then write down the complete equation of the straight line by using the calculated values of ( m and c ) into the general equation and express in form:

`y\text{ = m}\cdot x\text{ + c}`

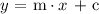
Where,

`m\text{ and c are calculated quantities!}`