Question

a pole is 3.4m tall casts a shadow that is 1.04m long. At the same time, a building casts a shadow that is 35.75m long. how tall is the building? round your answer to the nearest meter.

Answer 1

Height of the building is 117m.

Given:

Height of a pole is, h = 3.4m.

Length of the shadow of pole is, l = 1.04m.

Length of the shadow ofbuilding is, L = 35.75m.

The objective is to find the height of the building (H).

The given situation can be represented as,

Here, OA represents the height of the pole and OB represents the shadow of the pole.

Similarly, OC represents the height of the builiding and OD represents the shadow of the building.

Since, both shadow occurs at the same time, the angle of depressions angle A and angle C will be equal for both pole and the building.

It is known that is two of an angles of a triangles are equal, then the third side will also be equal.

By AAA criteria, both are similar triangles.

`\Delta AOB\approx\Delta\text{COD}`

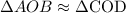
Then, the height of the building (x) can be calculated by Basic Proportionality theorem of similar triangles.

`(AO)/(CO)=(OB)/(OD)`

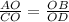
Now, substitute the given values in the above ratio.

`\begin{gathered} (3.4)/(x)=(1.04)/(35.75) \\ x=(35.75)/(1.04)*3.4 \\ x\approx117m \end{gathered}`

Hence, height of the building is 117m.