Question

The figure shows that a bicyclist tips the cycle when making a turn. The angle B, formed by the vertical direction and the bicycle, is called the banking angle. The banking angle varies inversely as the cycle's turning radius. When the turning radius is 4 feet, the banking angle is 30°. What is the banking angle when the turning radius is 7.5 feet?

Answer 1

Given the question in the question, the following are the solution steps to answer the question.

STEP 1: Write the relationship between the banking angle and the radius

STEP 2: Solve for the constant of variation from the inverse variation in step 1

`\begin{gathered} a\propto(1)/(r) \\ \text{Introducing the constant k} \\ a=(k)/(r) \\ By\text{ cross multiplication,} \\ ar=k \end{gathered}`

STEP 3: Get the value of k for the given radius and banking angle

`\begin{gathered} k=ar \\ a=30,r=4 \\ k=30*4=120 \end{gathered}`

STEP 4: Get the banking for the given turning radius

`\begin{gathered} k=ar \\ \text{k is constant and is 120} \\ r=7.5,a=\text{?} \\ By\text{ substitution,} \\ 120=a*7.5 \\ \text{Divide both sides by 7.5} \\ (120)/(7.5)=(a*7.5)/(7.5) \\ 16=a \\ a=16^(\circ) \end{gathered}`

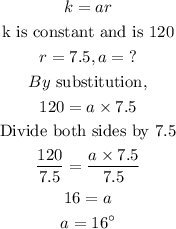
Hence, the banking angle for the given turning radius is 16 degrees