Lines a and b are parallel, you know that m∠2=63º and m∠9=105º
m∠2 and m∠5 are vertically opposite angles, which means that they are congruent, so that:
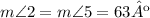
Now, looking at the angles formed when lines a and b are intersected by line c
The angle formed by the sum of m∠5 and m∠4 and the angle m∠9 are corresponding angles, which means that they are congruent, you can express this as follows:

Knowing the measures of m∠9 and m∠5 we can determine the measure of m∠4:

Finally, you have to look at the angles formed when line d crosses the lines a and b:
m∠4 and m∠13 can be linked with an F-shaped line, which indicates that they are corresponding angles. This means that they are congruent so that:
