Question

Use y = x^2 + 12x + 11(-2, -9) is a point on the graph. What point is the reflection of (-2,-9) across the axis of symmetry of the parabola?

Answer 1

The equation:

`y=x^2+12x+11`

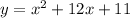
has the form:

`y=ax^2+bx+c`

with a = 1, b = 12 and c = 11.

The x-coordinate of the vertex, Xv, is found as follows:

`\begin{gathered} x_v=(-b)/(2a)_{} \\ x_v=(-12)/(2\cdot1) \\ x_v=(-12)/(2) \\ x_v=-6 \end{gathered}`

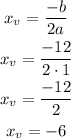
And the equation of the axis of symmetry of the parabola is:

`\begin{gathered} x=x_v \\ x=-6 \end{gathered}`

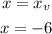
The point (-2, -9) is located 4 units to the right of the axis of symmetry. Then, the reflected point must be located 4 units to the left, its x-coordinate must be:

x = -6 - 4 = -10

Evaluating this point into the function:

`\begin{gathered} y=(-10)^2+12\cdot(-10)+11 \\ y=100+-120+11 \\ y=-9 \end{gathered}`

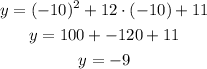
Therefore, the reflected point is (-10, -9).