Question

For the following exercise find the length of side x. round to the nearest tenth

Answer 1

The Law of Cosines is used to find the remaining parts of an oblique (non-right) triangle when either the lengths of two sides and the measure of the included angle is known (SAS) or the lengths of the three sides (SSS) are known.

The given figure has two sides and the included angle (SAS)

By law of cosines, we can solve this by

`c^2=a^2+b^2-2ab\cos C`

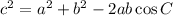
Let

a = 4.5

b = 3.4

c = x

∠C = 42°

Substitute the following and we get

`\begin{gathered} c^2=a^2+b^2-2ab\cos C \\ (x)^2=(4.5)^2+(3.4)^2-2(4.5)(3.4)\cos 42\degree \\ x^2=20.25+11.56-30.6\cos 42\degree \\ x^2=31.81-30.6\cos 42\degree \end{gathered}`

Get the square root of both sides

`\begin{gathered} \sqrt[]{x^2}=\sqrt[]{31.81-30.6\cos 42\degree} \\ x=3.011605608 \end{gathered}`

Rounding off to the nearest tenth, and the value of the length side x is equal to 3.0 units.