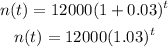Question

A park ranger has determined that the number of trees in his forest is increasing by 3% per year. In 2010, there were 12,000 trees in the forest. Write the equation that represents the number of trees n, in terms of t, the number of years since 2010.

Answer 1

Since the number of trees increases 3% each year, then

We will use the exponential function to represent this situation

`n(t)=a(1+r)^t`

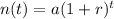
a is the initial value

r is the rate of increases in decimal

Since there were 12000 trees in 2010, then

a = 12000

Since the percent of increases is 3%, then

r = 3/100 = 0.03

Substitute them in the form of the equation above

`\begin{gathered} n(t)=12000(1+0.03)^t \\ n(t)=12000(1.03)^t \end{gathered}`