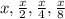Solution:
Concept:
We will first have to calculate the common ratio of the sequence and see the sequence that gives a common ratio of 1/2
From the first option
The formula given in the question is given below as
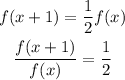
From the first option,
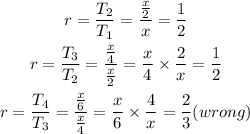
Hence,
The first option is wrong
From the second option,
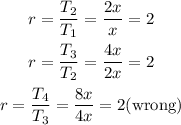
Hence,
The second option is wrong
From the third option,
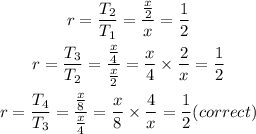
Hence,
The right answer is the third option