Question

ii ) Find the number of units that must be sold in order to yield the maximum profit?the first answer to the first question is 80 for maximum profit.

Answer 1

II) 80 units

Solving the II question:

1) Considering that the maximum profit is obtained by

P(x) = R(x) - C(x) Plugging into that those functions:

P(x) = 20x -0.1x²-(4x+2)

P(x) = 20x - 0.1x² -4x -2 Rewriting it

P(x)= -0.1x² +16x -2

2) The number of units that must be sold is the x-coordinate of the Vertex of that parabola since the Y-axis is the Profit P(x) and this is found by the following formula:

`X_V=-(b)/(2a)=(-16)/(2(-0.1))=(-16)/(-0.2)=80`

By the way, the Maximum profit (Question I), (Maximum point), on the other hand, is the Y-vertex:

`Y_V=(-\Delta)/(4a)=\frac{-(16^2-4(-0.1)(-2)_{}}{4(-0.1)}=638`

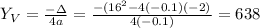
As we can see here:

3) Hence, the answer is 80 units that yield a maximum profit of $638