ANSWER
1.7, 1.72, 1.78, 16, 17, 18
Step-by-step explanation
We want to order the numbers from least to greatest.
We have:
18, 1.78, 16, 17, 1.7, 1 8/11
Convert 1 8/11 too decimal:
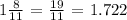
So, we have:
18, 1.78, 16, 17, 1.7, 1.72
Therefore, from least to greatest:
1.7, 1.72, 1.78, 16, 17, 18
That is the answer.