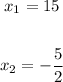Question

I don't understand how to solve the proportion.2x/x+3 = 25/x

Answer 1

Given the following proportion:

`(2x)/(x+3)=(25)/(x)`

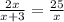
You can solve it by following the steps shown below:

1. You can multiply both sides of the equation by:

`x+3`

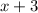
Then:

`\begin{gathered} (x+3)((2x)/(x+3))=((25)/(x))(x+3) \\ \\ 2x=(25(x+3))/(x) \\ \\ 2x=(25x+75)/(x) \end{gathered}`

2. Now you can multiply both sides of the equation by "x":

`\begin{gathered} (x)(2x)=((25x+75)/(x))(x) \\ \\ 2x^2=25x+75_{} \end{gathered}`

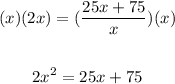
3. Rewrite the Quadratic Equation in the form:

`ax^2+bx+c=0`

Then:

`2x^2-25x-75_{}=0`

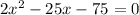
4. You can identify that:

`\begin{gathered} a=2 \\ b=-25 \\ c=-75 \end{gathered}`

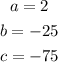
5. Then, you can use the Quadratic Formula to find the solutions:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Substituting values and evaluating, you get:

`\begin{gathered} x=\frac{-(-25)\pm\sqrt[]{(-25)^2-4(2)(-75)}}{(2)(2)} \\ \\ x=(25\pm35)/(4) \\ \\ x_1=(25+35)/(4)=15 \\ \\ x_2=(25-35)/(4)=(-10)/(4)=-(5)/(2) \end{gathered}`

Therefore, the answer is:

`\begin{gathered} x_1=15 \\ \\ x_2=-(5)/(2) \end{gathered}`