Given:
|x - 7| > 4
Let's solve the inequality for x using the following steps.
Step 1:
Find the inside of the absolute value when it is non-negative
x - 7 ≥ 0
Add 7 to both sides:
x - 7 + 7 ≥ 0 + 7
x ≥ 7
Find the inside of the absolute value when it is negative by multiplyin by -1:
-(x - 7) > 4
Step 2:
We have two conditions
x - 7 > 4
-(x - 7) > 4
Let's solve for x in both conditions.
We have:
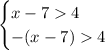
Condition 1:
x - 7 > 4
Add 7 to both sides:
x - 7 + 7 > 4 + 7
x > 11
Condition 2:
-(x - 7) > 4
Apply distributive property:
-x - - 7 > 4
-x + 7 > 4
Subtract 7 from both sides:
-x + 7 - 7 > 4 - 7
-x > -3
Divide both sides by -1:
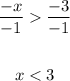
ANSWER:
x < 3 or x > 11