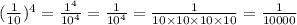We can express the number 0.1 as the quotient 1/10, then we get:
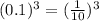
With quotients, we can distribute the power, and raise both the numerator and the denominator, like this:
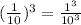
no matter what is the value of the power, every time you raise 1 to something, you get 1, then we get:
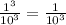
In this case, we have 10^3 in the denominator, this is the same as multiplying 10 3 times, like this:
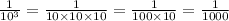
Then:
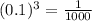
Similarly, with (1/10)^4: