Question

When the light ray illustrated in the figure below passes through the glass block of index of refraction n = 1.50, it is shifted laterally by the distance d. (Let L = 2.20 cm and = 28.0°.)(a) Find the value of d. in cm(b) Find the time interval required for the light to pass through the glass block. in ps

Answer 1

Part (a)

According to Snell's law,

`n_a\sin \theta=n\sin r`

Substitute known values,

`\begin{gathered} (1)\sin 28.0^(\circ)=(1.50)\sin r \\ \sin r=(0.469)/(1.50) \\ r=\sin ^(-1)(0.313) \\ =18.2^(\circ) \end{gathered}`

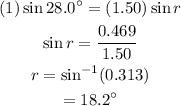
The lateral shift can be given as,

`d=(L)/(\cos r)\sin (\theta-r)`

Substituting values,

`\begin{gathered} d=\frac{2.20\text{ cm}}{\cos18.2}\sin (28.0-18.2) \\ =\frac{2.20\text{ cm}}{0.95}(0.170) \\ =0.394\text{ cm} \end{gathered}`

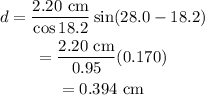
Thus, the value of d is 0.394 cm.

Part (b)

The time taken to pass through the glass is,

`t=(L)/(c)`

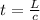
Substituting values,

`\begin{gathered} t=\frac{(2.20\text{ cm)(}\frac{1\text{ m}}{100\text{ cm}})}{3*10^8\text{ m/s}} \\ =(0.733*10^(-10)s)(\frac{1\text{ ps}}{10^(-12)\text{ s}}) \\ =73.3\text{ ps} \end{gathered}`

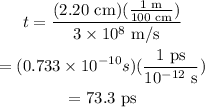
Thus, the time taken by light to travel is 73.3 ps.