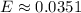Given that:
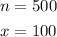
You need to use the following formula in order to calculate the Margin of error E:
![E=Z_{(a)/(2)}\sqrt[]{(pq)/(n)}](https://img.qammunity.org/2023/formulas/mathematics/college/638dhi12nrw2odxbts15m2lkcks9si14rm.png)
Where "p" is the probability of success, "q" is the probability of failure, "Z" is z-score, and "n" is the sample size.
In this case, since you need to use a 95% degree of confidence, by definition:
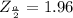
By definition:

Substituting the values of "n" and "x" into the first formula and evaluating, you get that:
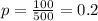
Therefore, "q" is:
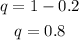
Knowing all those values, you can substitute them into the formula for calculating the Margin of Error:
![E=1.96\sqrt[]{((0.2)(0.8))/(500)}](https://img.qammunity.org/2023/formulas/mathematics/college/jrnp2w3wgmm1daf7mi8vwczwpzmudedsp8.png)
Finally, evaluating, you get:
![\begin{gathered} E=1.96\sqrt[]{(0.16)/(500)} \\ \\ E\approx0.0351 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/9547m1jmxllb9xcqnk3vy7puq5uynnk17r.png)
Therefore, the answer is: