1 Answer

IronSean · Answer 1 · 2023-02-27T18:50:21+0000

Given:

One friend heads north 20 miles per hour.

Other heads East 50 miles per hour.

let r be the number of hours traveled.

After t hours the distance traveled by the first friend is

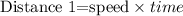
$\text{Distance 1=speed}* time$

Substitute speed=20 and time =t, we get

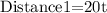
$\text{Distance1=20t}$

After t hours the distance traveled by the second friend is

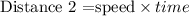
$\text{Distance 2 =speed}* time$

Substitute speed=50 and time =t, we get

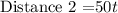
$\text{Distance 2 =}50t$

Using the Pythagoras theorem to find the distance between two friends.

Distance between two friends is

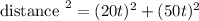
$\text{distance }^2=(20t)^2+(50t)^2$

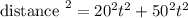
$\text{distance }^2=20^2t^2+50^2t^2$

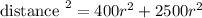
$\text{distance }^2=400r^2+2500r^2$

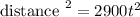
$\text{distance }^2=2900t^2$

Taking square root on both sides, we get

$\text{distance }=\sqrt[]{2900t^2}$

$\text{distance }=10\sqrt[]{29}t$

Hence the required distance is

$\text{distance }=10\sqrt[]{29}.t$

Please log in or register to add a comment.