Question

Prove that the median to the hypotenuse of a right triangle is half the hypotenuse

Answer 1

To compare lengths, use the distance formula (2nd option)

Step-by-step explanation:

We want to prove OP = 1/2 MN

We need to find the midpoint of MN which is point P

Using the midpoint formula:

`$$\text{Midpoint = }(1)/(2)(x_1+x_2),\text{ }(1)/(2)(y_1+y_2)$$`
`\begin{gathered} M\text{ }(0,\text{ 2b})\text{ and N }(2a,\text{ 0}) \\ x_1=0,y_1=2b,x_2=2a,y_2\text{ = 0} \\ Midpoint\text{ P = }(1)/(2)(0\text{ + 2a}),\text{ }(1)/(2)(2b\text{ + 0}) \\ Midpoint\text{ P = }(1)/(2)(2a),\text{ }(1)/(2)(2b) \\ Midpoint\text{ P = a, b} \end{gathered}`

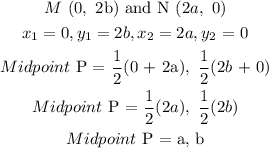
Since P is the midpoint of MN, it means:

MP = NP

We need to ascertain OP = 1/2 MN

To do this, we will use the distance formula:

`$$dis\tan ce\text{ = }\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2}$$`
`\begin{gathered} distance\text{ OP: O}(0,0)\text{ and P}(a,\text{ b}) \\ O\text{ is from the origin. Coordinate = }(0,\text{ 0}) \\ x_1=0,y_1=0,x_2=a,y_2\text{ = b} \\ distance\text{ OP = }\sqrt{(b\text{ - 0})^2+(a-0)^2}\text{ } \\ distance\text{ OP = }√(b^2+a^2) \end{gathered}`
`\begin{gathered} distance\text{ MN: M}^(0,\text{ 2b})\text{ and N }(2a,\text{ 0}) \\ x_1=0,y_1=2b,x_2=2a,y_2\text{ = 0} \\ distance\text{ MN = }\sqrt{(0-2b)^2+(2a\text{ - 0})^2}^ \\ distance\text{ MN}=\text{ }√((-2b)^2+(2a)^2)\text{ = }√(4b^2+4a^2) \\ distance\text{ MN = }√(4(b^2+a^2))\text{ } \\ distance\text{ MN = 2 }\sqrt{b^2+\text{ a}^2} \end{gathered}`
`\begin{gathered} half\text{ of distance MN = }(1)/(2)(2\text{ }√(b^2+a^2)) \\ half\text{ of distance MN = }√(b^2+a^2) \end{gathered}`

From our result above, OP = 1/2 MN

To compare lengths, use the distance formula (2nd option)