Question

Options for the first box: x, x+10, 3x(x+10), x(x+10) Options for the second box are 1, 0, and 2

Answer 1

The least common denominator or the LCD of the given equation is the smallest number that can be a common denominator for the set of fractions. Usually, to get the LCD, we would multiply the denominators in the set of fractions.

Since the denominators are x, x + 10, and 3, we will multiply this and the LCD is 3x(x+10).

For the number of valid solutions, let's solve it and find how many,

`\begin{gathered} (1)/(x)+(2)/(x+10)=(1)/(3) \\ (x+10+2x)/(x(x+10))=(1)/(3) \\ (3x+10)/(x^2+10x)=(1)/(3) \\ 3(3x+10)=1(x^2+10x) \\ 9x+30=x^2+10x \\ 0=x^2+10x-9x-30 \\ x^2+x-30=0 \\ (x+6)(x-5)=0_{} \\ x=-6 \\ x=5 \end{gathered}`

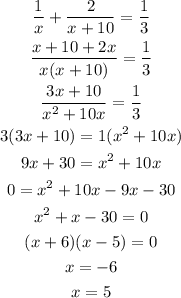
Since there are two possible values of x, then there are 2 valid solutions.