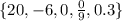SOLUTION
Given the question in the question tab, the following are solution steps to get the elements of B that belong to the given set.
Step 1: Define rational numbers
A rational number is a number that can be expressed in the form of p/q, where p and q are integers and q is not equal to 0. Non-terminating decimals that do not have repeated numbers after the decimal point are not rational numbers.
Step 2: Write out the given sets
![\begin{gathered} B=\mleft\lbrace20,\sqrt[]{8,}-6,0,(0)/(9),0.3\mright\rbrace \\ Rational\text{ numbers=}*\mleft\lbrace(p)/(q)\mright|p,q\text{ are real numbers},and\text{ q}\\e0\} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2yc3baaq561s3v7fzwl1xlwdjongmbgjyr.png)
Step 3: Write out the rational numbers from set B
![\begin{gathered} 20\text{ }\epsilon Rational\text{ numbers (because it can be written in the }(p)/(q)\text{ as in }(20)/(1)) \\ \sqrt[]{8}\text{ is not a rational number because the solution gives a non-terminating decimal with non repeating digits} \\ -6\text{ }\epsilon Rational\text{ numbers (because it can be written in the }(p)/(q)\text{ as in }(-6)/(1)) \\ 0\text{ }\epsilon Rational\text{ numbers (because it can be written in the }(p)/(q)\text{ as in }(0)/(1)) \\ (0)/(9)\text{ }\epsilon Rational\text{ numbers (because it can be written in the }(p)/(q)\text{ }) \\ 0.3\text{ }\epsilon Rational\text{ numbers (because it can be written in the }(p)/(q)\text{ as in }(3)/(10)) \end{gathered}]()
Hence, it can be seen from the explanations in Step 3 that the following are rational numbers:
Option B: