13)T=-4.5e+103
14)when the elevation is 20000 ft, the temperature is 13 °
Step-by-step explanation
Step 1
set the points
so, let
hence,
6000 ft= 6 thousands ft
12000 ft=12 thousands ft
P1(6,76)
P2(12,49)
Step 2
find the slope of the line:
the slope of the lines is given by the expression
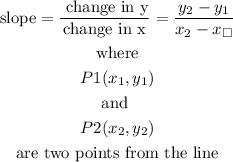
replace with P1 and P2 from the previous step

therefore, the slope is -4.5
Step 3
finally, get the equation
we can use the point-slope form and the, isolate y
so
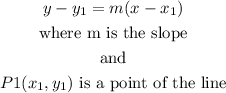
then ,let
P1(6,76)
slope=-4.5
replace

therefore, using T as the temperature and e as the elevation, we have
T=-4.5e+103
Step 4
(14)
now, we have to predict the temperature when the elevation is 20000 ft
so
let
e=20 thousand ft
T=?
replace in the equation we found
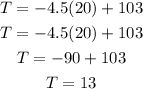
therefore, when the elevation is 20000 ft, the temperature is 13 °
I hope this helps you