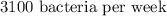Answer:
The average rate of change for the first five weeks of population growth is;
Step-by-step explanation:
Given that the growth of a population can be modeled by the exponential function;
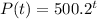
The average rate of change for the first five weeks can be calculated using the formula;
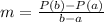
For the first five weeks;
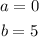
substituting to get the value of the function at this points;

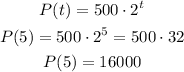
So, the average rate of change is;
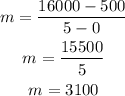
Therefore, the average rate of change for the first five weeks of population growth is;