Function 1 and function have the same rate of change.
The rate of change for the function 2 is the slope m = 5( The coefficient of x)
For the function 1:
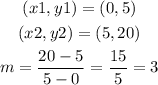
Since:
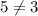
They dont have the same rate of change.
----------------------
The functions have the same value when x = 5.
For function 1:
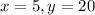
For function 2:
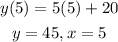
They have different values.
-----------------------------------
The sum of the rates of change for both functions is 8

This is true