Question

Find the equation of the line shown in the graph. Write the equation in slope-intercept form. Y=

Answer 1

`y=(1)/(2)x-1`

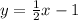
Step-by-step explanation

the slope-intercept form of a line is

`\begin{gathered} y=mx+b \\ \text{where m is the slope and b is the y-intercept} \end{gathered}`

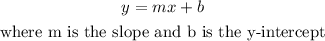
Step 1

find the slope of the line:

the slope of a line is given by:

`\begin{gathered} \text{slope}=\frac{change\text{ in y}}{\text{change in x}}=(\Delta y)/(\Delta x)=(y_2-y_1)/(x_2-x_1) \\ \text{where} \\ P1(x_1,y_1) \\ \text{and} \\ P2(x_2,y_2) \\ \text{are 2 points from the line} \end{gathered}`

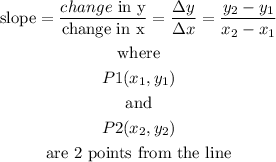
then

pick 2 points from the line:

let

P1(0,-1)

P2(2,0)

now, replace and get the slope

`\begin{gathered} \text{slope}=(y_2-y_1)/(x_2-x_1) \\ \text{slope}=(0-(-1))/(2-0)=(1)/(2) \end{gathered}`

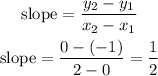
so, the slope (m) is 1/2

Step 2

now, we need the y-intercept(b), if we have the graph, the simplest way to find the y-intercept is by watching the point where the line crosses the y-axis, in this case

`y-\text{intercept}=-1`

so, we have

slope=m=1/2

y-intercept=-1

replace

`y=mx+b\rightarrow y=(1)/(2)x-1`

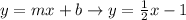
so, the answer is

`y=(1)/(2)x-1`

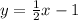
I hope this helps you