Question

Type the correct answer In each box. Use numerals Instead of words. If necessary, use / for the fraction bar(s). Rewrite the following equation in the form Y=(a(x-h)^2+k Then, determine the x-coordinate of the minimum.
`y2 {x}^(2) * 32 x + 56`The rewritten equation is Y= _____(x-____)^2 +____The x-coordinate of the minimum Is ____//

Answer 1

We are given the following quadratic equation

`y=2x^2-32x+56`

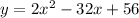
We are asked to convert this equation into the vertex form given by

`y=a(x-h)^2+k_{}`

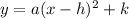
Let us convert the given quadratic equation into the above form.

`\begin{gathered} y=2x^2-32x+56 \\ y-56=2x^2-32x \\ y-56=2(x^2-16x) \end{gathered}`

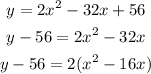
Now we have to add a number to both sides of the equation such that the terms inside the parenthesis become perfect squares.

How about 64?

`y-56+128=2(x^2-16x+64)`

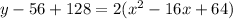
Why did we add 128 on the left side?

Because 64 is being multiplied by 2 on the right side of the equation so 64x2 = 128

`\begin{gathered} y-56+128=2(x^2-16x+64) \\ y+72=2(x-8)^2 \\ y=2(x-8)^2-72 \end{gathered}`

As you can see, the equation has been converted into the vertex form.

Finally, the x-coordinate of the minimum is

The value of h is the x-coordinate of the minimum and the value of k is the y-coordinate of the minimum

Comparing the above equation with the standard vertex form, we see that

h = 8

Therefore, 8 is x-coordinate of the minimum