Question

Compare P(Grade 12 | opposed with P(opposed | Grade 12). (1 point)

Answer 1

Given that the table that shows the results of the survey, you can identify that the total number of students surveyed is:

`Total=5+3+9+8+12+9+15+16+10+12+6+11=116`

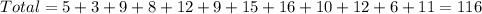
Let be:

- Event A: Grade 12.

- Event B: Opposed.

You need to use the Conditional Probabilty Formula:

`P(A|B)=(P(A\cap B))/(P(B))`

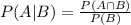
• You need to find:

`P(A\cap B)`

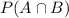
You can identify in the table that the number of students that belong to Grade 12 and Opposed is:

`6`

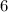
Therefore:

`P(A\cap B)=(6)/(116)=(3)/(58)`

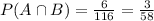
The number of students that belong to Opposed is:

`Opposed=3+12+16+6=37`

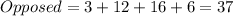
Therefore:

`P(B)=(37)/(116)`

Now you can determine that:

`P(A|B)=((3)/(58))/((37)/(116))=(6)/(37)`

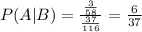
• You need to find:

`P(B|A)`

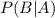
Use:

`P(B|A)=(P(A\cap B))/(P(A))`

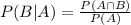
You can determine that:

`P(A)=(12+6+11)/(116)=(29)/(116)=(1)/(4)`

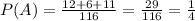
Finally:

`P(B|A)=((3)/(58))/((1)/(4))=(6)/(29)`

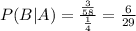
Notice that:

[tex]P(A|B)

Hence, the answer is: Third option.