Question

0,0,0,2,3,4,7,7,8,12,14,15,15,16,18 quartile 1 = quartile 2= interquartile range=

Answer 1

The IQR describes the middle 50% of values when ordered from lowest to highest.

Given a dataset, to find the interquartile range ​first find the median (middle value) of the lower(first quartile) and upper half of the data(third quartile), and then find their difference.

Our dataset is

`\lbrace0,0,0,2,3,4,7,7,8,12,14,15,15,16,18\rbrace`

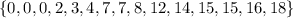
We have 15 elements on this dataset. The median is the value separating the higher half from the lower half of a data sample, a population, or a probability distribution. Since we have 15 elements, the middle element is the 8th element(this way we have 7 elements below and 7 elements above our median). The 7 elements below are

`\lbrace0,0,0,2,3,4,7\rbrace`

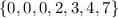
The median of those points are the first quartile. The median of this dataset is 2.

For the upper half of the data, we have

`\lbrace8,12,14,15,15,16,18\rbrace`

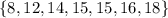
The median is 15, therefore, the third quartile is 15.

The interquartile range is the difference between those values.

`15-2=13`

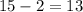
The IQR of our dataset is 13.