Question

To be ADA compliant, wheelchair ramps require no more than a 4.8 degree slope for the ramp. How long in feet would a ramp need to be to reach a porch that is 36 inches above the ground? If ramps can be no longer than 30 feet. Can just one ramp be built to reach the porch or would a landing and another ramp be needed to stay ADA compliant? Show and explain your work using mathematical language from this course.

Answer 1

We have to find the length of a ramp with the allowed slope that reaches a porch that is 36 inches above the ground.

We can draw this ramp as:

As this is a right triangle, we can use trigonometric ratios to relate the length, the height and the angle.

We can then write:

`\begin{gathered} \tan(4.8\degree)=(Opposite)/(Adyacent) \\ \tan(4.8\degree)=(h)/(L) \\ L=(h)/(\tan(4.8\degree))\approx(36)/(0.084)\approx429 \end{gathered}`

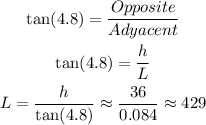
This length is expressed in inches, so we can convert it to feet as:

`L=429\text{ in}\cdot\frac{1\text{ ft}}{12\text{ in}}=35.75\text{ ft}`

As this length is longer than what is allowed by the norm (the length has to be at most 30 feet), we will need more than one ramp to stay ADA compliant.

Answer:

The ramp with a slope of 4.8° would have to be 35.75 ft long.

It will need more than one ramp to stay ADA compliant.