Question

Examine the diagram of chord LM in •P at right. If the length of the radius of •P is 6 units and if measure of arc LM = 150°, find LM. What if you know the length of a chord? How can you use it to reverse the process? Draw a diagram of a circle with radius with length 5 units and chord AB with length 6 units. Find the measure of arc AB.

Answer 1

• (a)The length of LM is 11.59 units.

,

• (b)The measure of arc AB is 73.74 degrees.

Explanation:

Part A

Given that:

• The measure of arc LM=150°

,

• Radius of circle P = 6 units.

To find the length of LM, follow the steps below:

Draw a perpendicular line from the centre, P to the chord LM as shown below:

This line bisects LM and the angle at P.

We can then find x in the diagram.

`\begin{gathered} \sin75\degree=(x)/(6) \\ x=6\sin75\degree \end{gathered}`

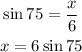
Multiply the result by 2 to get LM.

`\begin{gathered} LM=2x=2*6\sin75\degree \\ LM\approx11.59\text{ units} \end{gathered}`

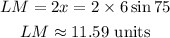
The length of LM is 11.59 units.

Part B

Let the center of the circle = O

• The radius of circle O = 5 units

,

• Length of chord AB = 6 units

The diagram showing this is attached below:

To find the measure of arc AB, follow a reverse process.

Draw a perpendicular line from O to AB. That line divides AB into two equal parts of 3 units each.

We then find the indicated angle.

`\begin{gathered} \sin\theta=(3)/(5) \\ \implies\theta=\arcsin((3)/(5)) \end{gathered}`

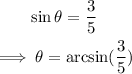
Therefore, the measure of arc AB will be:

`m\widehat{AB}=2*\arcsin((3)/(5))=73.74\degree`

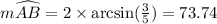
The measure of arc AB is 73.74 degrees.